编者按：生活中处处充满了优化，但如何将具体问题转化为合理的数学模型并求得极值却一直困扰着学界。提到求极值很容易会想到函数求导，然而实际问题的数学模型很可能是非凸非线性，还可能会涉及到主观控制，甚至一些问题无法用准确的数学模型进行描述，对于这类问题我们无法通过单纯的求导来获得极值。而贝叶斯优化对函数f(x)没有硬性要求，仅仅通过少量的采样点便可以进行推测函数的极值，因此受到了广泛的认可与应用。

作者：张楚珩
（清华大学 交叉信息院博士在读）

最近有做离子阱实验的同学涉及到一些实验参数的调参问题，其中主要需要用到贝叶斯优化。同时，我自己在想的一些问题也可能会用到贝叶斯优化。

1. 问题设定

贝叶斯优化主要解决一个优化问题，即

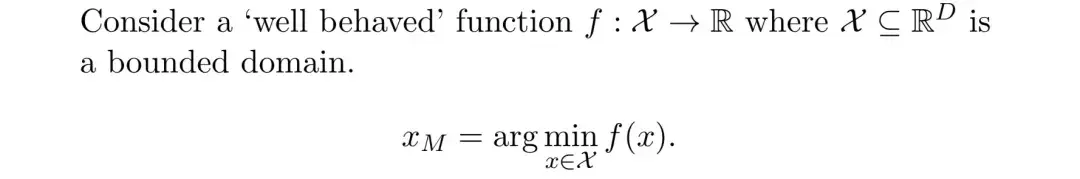
该待优化函数具有如下特点：

? Expensive to evaluate：每次给定一个x 来获取f(x)数值都有一定的成本，因此目标是尽可能少地去采样而找到一个好的解。

? Black box：它不具有一些特殊的结构性质，比如 convexity、linearity 等，因此有一些能够针对这些结构特性来加速优化的方法不能被使用；

? Derivative-free：无法获得它的导数，即不能使用一些基于导数来加速优化的方法；

? (Maybe) noisy：对于函数f的一次采样得到的数值可能包含一个均值为零的噪声，因此即使在某一个点上也不能完全相信采样得到的数值；

该设定有着广泛的应用。比如在离子阱的实验中，需要调节激光器的各种参数，从而形成一个由电磁波产生的“陷阱”从而“困住”离子，而实验的目标是需要让激光形成一个足够好的“陷阱”使得被困住的离子的温度（能量）能够足够低。该系统中x就是相应的激光器参数，f(x)就是相应参数下形成离子阱的温度。每组实验测试需要花费几十分钟的时间（expensive to evaluate），因此不能测试很多参数；该过程涉及到非常多的物理过程而几乎无法解析地求解，因此只能把它当做一个黑盒子来优化（black box）。

对于该类问题，有一些比较 naive 的解法，比如使用先验知识来确定参数（玄学）、使用 grid search（维度爆炸）、使用 random search（效率低）。因此，我们需要使用贝叶斯优化的方法来有效地优化这类问题。

2. 贝叶斯优化的基本成分

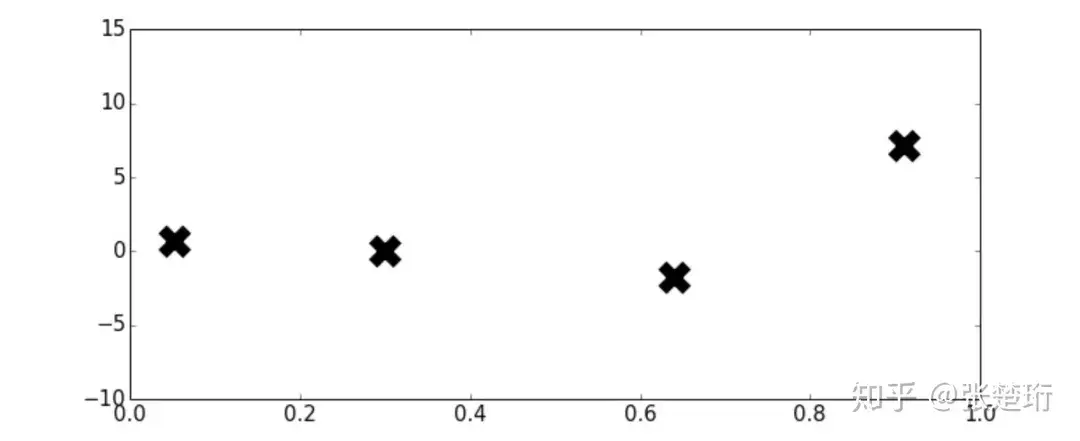
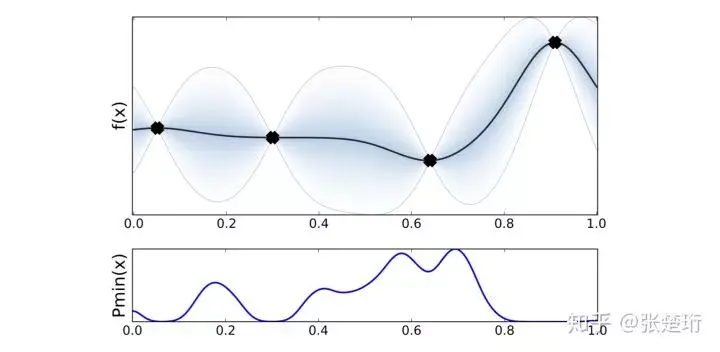
考虑如下一个例子，希望在[0,1]区间上找到使得函数f(x)取最小值的位置，函数f(x)是 L-Lipschitz 的，并且是可导的；而所有的信息只有四个位置上的f(x)值，如下图所示。

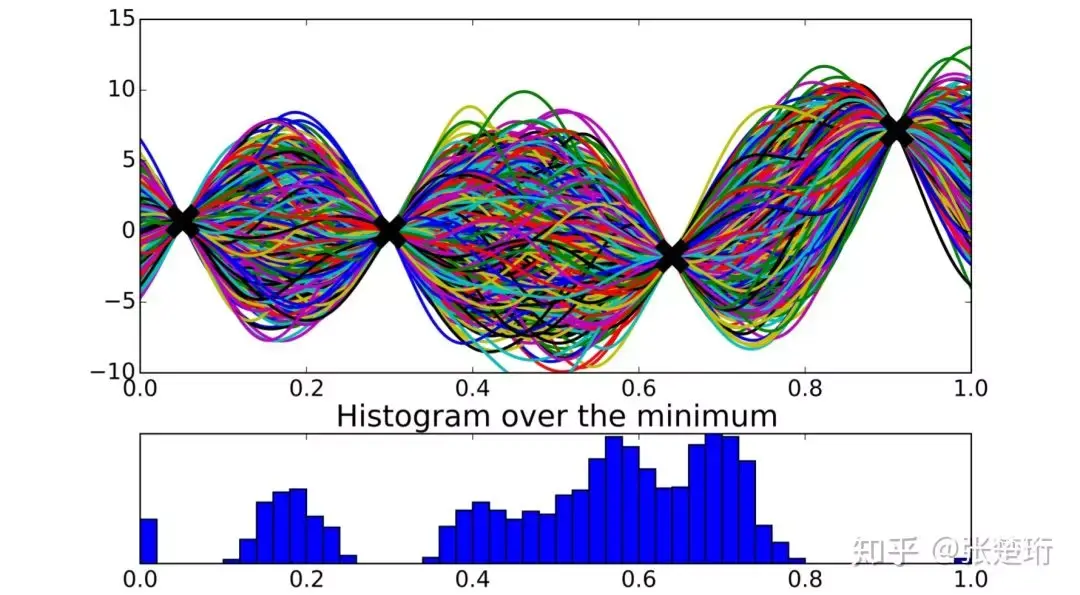
最简单的想法，就是把对于所有满足约束条件的函数进行采样，然后分别找出这些函数的最小值位置，把最常出现位置作为预测的最小值位置。如下图所示。

贝叶斯优化主要包括如下部分

? Prior: 确定函数f(x)的先验分布;

? Initial space-filling experimental design: 在函数的定义域上找一些尽可能分布均匀的初始点，并且得到它们相应的函数值；

? Posterior：通过一些概率模型（statistical model）根据已有的数据点来确定函数f(x)的后验分布；

? Acquisition function：根据求得的后验分布来确定下一个（或者下一批）实验点。

以上过程可以概括为如下算法框架。

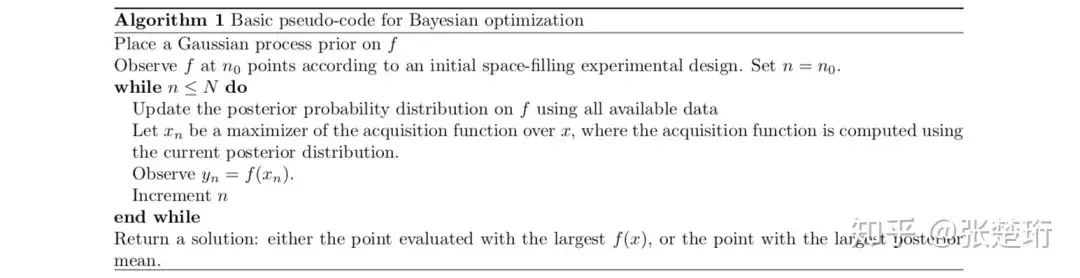
下面就这几个部分来具体讲解。

3. Statistical model

概率模型最常用的还是高斯过程（Gaussian process），当然也有其他的模型，比如 random forest、t-student process。这里只讲高斯过程。

4. Acquisition functions

Expected Improvement（EI）

因此，选择下一个试验点，使得该改善的期望最大。据此写出相应的 acquisition function

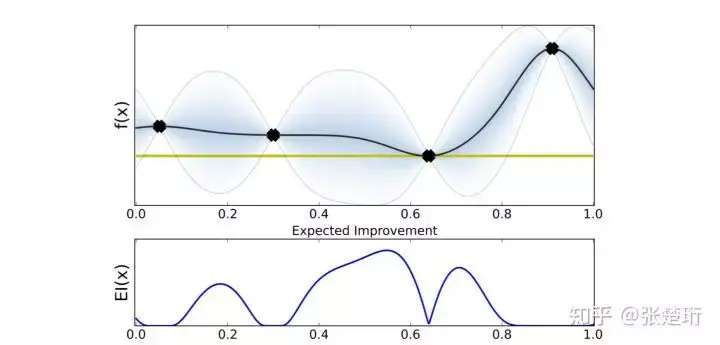
Maximum probability of improvement（MPI）

这是最早被提出的一种 acquisition function。和前一种不同的是，它最大化的是下一个采样点能够产生非零 improvement 的概率，即

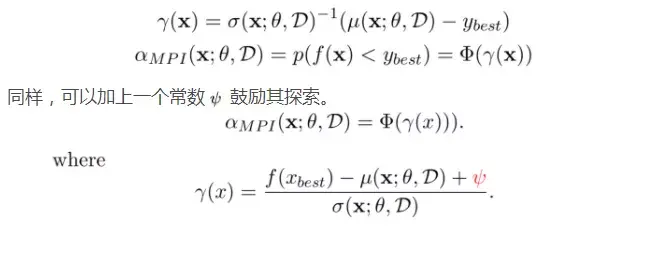
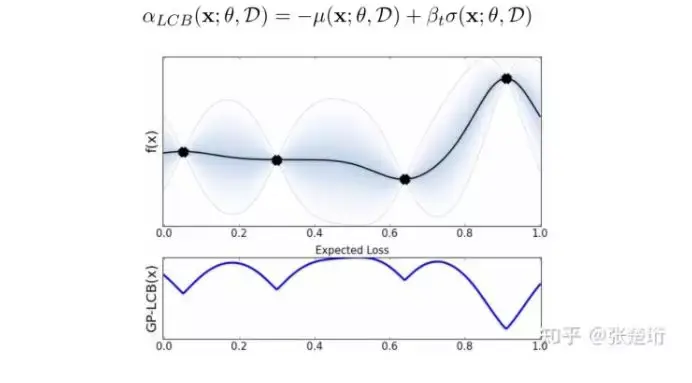
Lower confidence band（LCB）

其 acquisition function 如下

Knowledge gradient（KG）

Entropy search（ES）

其思想是希望找到一个样本点，使得得到改样本点的函数值之后，能够最大程度地更容易确定最优值的位置。即

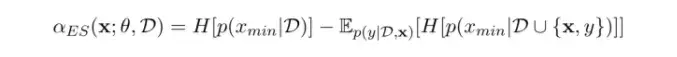
其缺点是上述公式不能够直接计算，需要通过采样的方式来近似计算。

Predictive entropy search（PES）

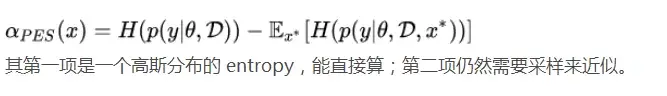
5. Initial space-filling experimental design

最开始需要选择一些样本点，作为算法的初始样本数据，这部分数据选择的目标是尽可能“均匀”地分布在感兴趣的区域内。

有如下一些方法

前两种方法比较 naive，没啥好解释的。

Latin design

主要是希望每一行（不同的样本）每一列（不同的维度）上的数值都尽可能散开。形象地来说就是下面这样

具体的实现可以参考 pyDOE: Randomized Designs。

(https://pythonhosted.org/pyDOE/randomized.html#latin-hypercube)

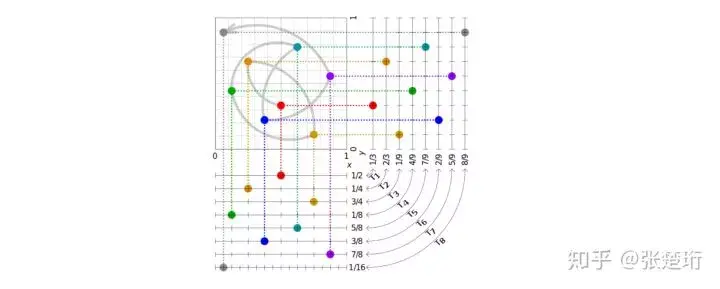
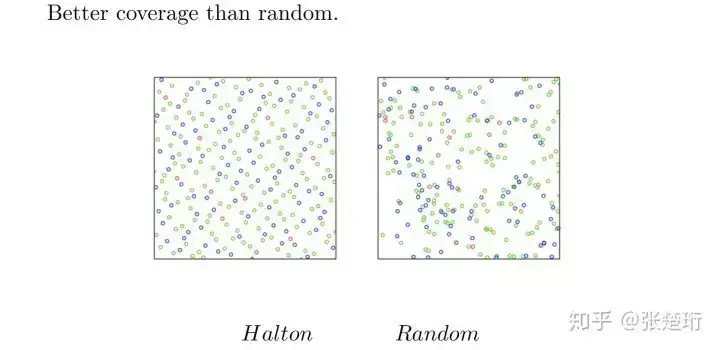
Halton sequences

通过下面的这种规律来生成样本点，使得生成的点更为均匀地分布在空间中。

6. 优化方法

7. 贝叶斯优化的推广

以下几方面的扩展也是目前贝叶斯优化研究比较多的方向：

? Multi-fidelity and multi-information source evaluation：考虑到实际中可能对于函数 的估计会有一些替代的方案。比如在神经网络超参调节上，可以在整个验证集上进行 evaluate，这样得到的估计比较准确，但是代价会比较大；也可以在部分验证集上进行 evaluate，这样估计的方差可能比较大，但是速度会比较快。该设定在我同学的离子阱实验中也存在，比如可以通过 CCD 拍到的照片大致判断温度的好坏（比如照片上有没有形成类似晶格的结构），也可以通过进一步的实验来直接确定离子阱的温度，但这样实验就会更复杂。这一类拓展就是在研究这个问题，在给出下一个试验点的同时，也希望给出一个方案，告诉我们下一个试验点使用怎样的实验条件来测量。

? Random environmental conditions and multi-task Bayesian optimization：有时候我们希望优化在各种实验条件下的平均性能，即

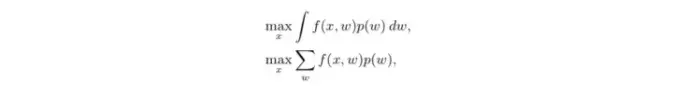
注意到其中 w 为控制不同实验环境的参数。这种情况下，其实可以对于每个试验参数 x 都在不同的环境下测试，然后求和作为 f(x) ，但是这样效率显然不够高。这种拓展条件下，会研究更有效率的方法。

参考文献：

[1]Bishop, Christopher M.Pattern recognition and machine learning. springer, 2006. Chapter 6.4 Gaussian Process

--------相关文章推荐--------

贝叶斯优化现今已经广泛运用到工业和生活的各个领域。本文立足于生活，讲述了如何通过贝叶斯优化来挑选西瓜。

点击蓝字标题，即可阅读《【AI】用贝叶斯方法挑西瓜》

其他

优化∣浅析黑洞成像背后的稀疏重构算法原理

优化 | 优化理论能给深度学习带来怎样的革命？

【优化】为什么凸优化这么重要？

加入『运筹OR帷幄』知识星球的好处

• 中国你能说出名字的几乎所有大厂（资深）算法工程师入驻
• 欧美数家大厂（资深）软件工程师入驻
• 以上所有公司独家内推机会
• 简历修改指导
• 面试咨询， 模拟面试
• 得到一对一指导、解答工作中的疑惑
• 多家Offer选择指导
• 以面试题为学习资料学习真正的算法干货，从小白变成大咖
• 不定期的线上、线下交流会和聚会,拓展人脉。